有趣啊,都已经到NOI的难度了,救命
首先,我们先讲述一下前置知识。已经明白的读者请移步后文
定义:\(z = a + bi\),其中 \(a, b \in R\ \ i = \sqrt{-1}\)
运算原则:
所以说,一个复数也可以写作 \(z = re^{i\theta}\) 的形式。
其中 \(r\) 为它的模,\(\theta\) 为它的辐角。
于是两个复数相乘也就相当于模相乘,辐角相加:
\[z_1 z_2 = r_1r_2 e^{i(\theta_1 + \theta_2)} \]
证明:
我们通过欧拉公式在 \(0\) 处展开:
那么我们考虑如何把三者扯上关系呢?
由于已知 \(i^2 = -1, i^3 = -i\) 那么我们先考虑 \(e^{ix}\)
那么,很明显, \(e^{ix} = \cos x + i \sin x\)
得证。
在 C++ 中我们其实可以直接使用 std::complex<double>。
文档可以参考 std::complex - cppreference.com
但是毕竟是 stl,其使用细节肯定没有那么顺手,而且实测很慢,所以建议手写复数模板。
考虑到实际中我们几乎不需要用到除法,所以,我们仅实现三则运算。
struct Complex {
double real, imag;
Complex() : real(0), imag(0) {}
Complex(double re, double im) : real(re), imag(im) {};
inline Complex operator + (const Complex & b) {
return Complex(real + b.real, imag + b.imag);
}
inline Complex operator - (const Complex & b) {
return Complex(real - b.real, imag - b.imag);
}
inline Complex operator * (const Complex & b) {
return Complex(real * b.real - imag * b.imag, real * b.imag + imag * b.real);
}
};
复制快速傅里叶变换的核心就是利用的单位根的一些独特的性质来快速实现的
单位根的定义:方程 \(z^n = 1\) 在复数范围内的 \(n\) 个根。
那么,不经过证明的给出,每一个根应该为 \(e^{i\frac{2k\pi}{n}}\)。
这里我们记 \(\omega_n\) 为主 \(n\) 次单位根, \(\omega_n^k = e^{i\frac{2k\pi}{n}}\)
举个例子,主 \(8\) 次单位根的 \(8\) 个值改写为形如 \((r, \theta)\) 的极坐标后,位置类似于下图:

证明:考虑展开即可:\(\omega_{dn}^{dk} = e^{i\frac{2dk\pi}{dn}} = e^{i\frac{2k\pi}{n}} = w_n^k\)
这个引理是快速傅里叶变化的核心
证明:也是考虑展开
证明:
根据等比数列公式
得证
(OI中)一般形式:\(F(x) = a_0 + a_1x + a_2 x^2 + \cdots + a_n x^n\)
上述多项式为一元多项式。
我们可以改写上式:\(\sum_{i=0}^n a_ix^i\)
我们对于多项式运算定义如下:
一般情况下,我们可以通过补零的方式,将两个次数不同的多项式调整到次数相同。这里我们都补充到 \(n\) 的长度
我们称这个系数向量 \(c\) 为向量 \(a, b\) 的卷积,记作 \(a \otimes b\)
表示方法
系数表示
它将一个多项式表示成由其系数构成的向量的形式
例如 \(A = [a_0, a_1, a_2, \dots, a_n]^T\)
加法即为 \(A_1+ A_2\),直接相加即可。时间复杂度 \(O(n)\)
乘法则做向量卷积,为 \(A_1 \otimes A_2\)。一般来说,时间复杂度为 \(O(n^2)\)
如果给定 \(x\) 求值,则可以使用霍纳法则或者秦九昭算法。时间复杂度为 \(O(n)\)
点值表示
用至少 \(n\) 个多项式上的点来表示
一般形式如 \(\{(x_0, A(x_0)), (x_1, A(x_1), \dots, (x_n, A(x_n))\}\)
进行运算是,一般要保证两个多项式在同一位置取值相同,即 \(x_i\) 相同
加法运算直接将两点坐标相加即可,时间复杂度为 \(O(n)\)
乘法运算只需要将两点纵坐标相乘即可。时间复杂度为 \(O(n)\),太好了!
如果我们需要 \(A(x)\) ,这个过程叫做插值,可以通过拉格朗日插值公式进行计算,复杂度为 \(O(n^2)\),这里不展开讲述。
DFT(Discrete Fourier Transform) 是快速傅里叶变换(FFT)的基础,也是快速数论变换(NTT)的基础
变换操作是对于一个向量而言(也就是多项式的系数表示法)
这个变换操作相当于求出这个多项式在 \(x\) 为单位根时的取值。
不妨设这个向量为 \(C = [c_0, c_1, c_2, \dots, c_{n-1}]^T\)
我们定义一个变换公式为
那么变换过后的序列为
其中 \(\omega\) 代表主 \(n\) 次的单位根。
或者我们可以通过矩阵来表示:
所以说,暴力的算法为 \(O(n^2)\),不如直接算。
对于上述序列,我们称形如 \(h(\omega^k)\) 的项为 \(k\) 次离散傅里叶级数。
我们将每一项展开,那么可以得到下图:

图片来自网络
这个时候,我们变换后的序列就是用点值表示的序列。
两个变换后的序列相乘,一一对应的乘法即可。
为什么?
变换后的序列其实就是函数在 \(w^0, w^1, \cdots , w^{n-1}\) 的点上的取值。
那么根据点值表示的多项式,两个多项式相乘,即是对应点相乘。
于是得到了两个多项式乘积的点值表示。
对于上述序列,其 \(-k\) 次离散傅里叶变换后的的值恰为 \(n \times c_k\)。
证明:
我们用 \(g(\omega^{-k})\) 表示变换后的结果
我们分类讨论一下:
\(j = k\),那么此时 \(\sum_{j=0}^{n-1} \omega^{(j-k)y} = \sum_{j=0}^{n-1} \omega^0 = n\)。对于 \(c_k\) 做出的贡献为 \(n\)
\(j \ne k\),将 \(k\) 看作常数,那么此时 \(\sum_{j=0}^{n-1} \omega^{(j-k)i} = \sum_{j=0}^{n-1} \omega^{j}\)。依据上文中求和引理,其值为 \(0\),也就是对 \(c_j\) 做出的贡献为 \(0\)。
综上所述,只有 \(c_k\) 对于答案做出了 \(n\) 次贡献,所以 \(g(\omega^{-k}) = n \times c_k\)
于是,我们可以得出两个多项式卷积的计算方法:
将两个多项式改写为向量的形式,并分别对其做一次离散傅里叶变换 (DFT)
将变换过后的两个序列相乘(点对点相乘)得出一个新的序列
我们再对此序列做一次逆傅里叶变换,也就是将序列变为 \(<g(\omega^{-0}), g(\omega^{-1}),g(\omega^{-2}), \dots, g(\omega^{-(n-1)})>\)
也就是 \(<n \times c_0, n \times c_1, \dots, n \times c_{n-1}>\)
最后对于每一项除以 \(n\) 即可。
但是:
最朴素的 DFT 变化的时间复杂度为 \(O(n^2)\),三次变换还不如直接暴力计算……所以我们就需要快速傅里叶变换来优化了。
FFT \(\to\) Fast-Fast-TLE
我们对于 \(f(x) = c_0 + c_1 x + c_2 x^2 + \dots + c_{n-1}x^{n-1}\),分离其奇数项和偶数项,构造出另外两个向量
那么,不难发现:
也就是说
补充一个点:
\[\omega_n^{\frac n2} = -1 \]证明:考虑我们在上面画出的图中,\(\omega_n^{\frac n2}\) 所在的位置。就是 -1 了
再根据单位根的消去原理稍微化一下……
于是,我们就可以递归分治了。
其时间为 \(T(n) = 2T(n/2) + O(n)\)
故复杂度为 \(T(n) = O(nlogn)\)。
其实我们还要考虑一点,我们要保证长度为 \(2^k\) 才能保证可以正确的分治
因为只有长度相等的区间才能合并(考虑此时单位根才一样)。
所以说,我们要把两个多项式通过补 \(0\) 的方式补齐到 \(2^k\) 项,合并之后就是 \(2^{k+1}\) 项。
对于模板题:【模板】多项式乘法(FFT) - 洛谷
可以写出如下龟速代码:
#include <iostream>
#include <algorithm>
#include <vector>
struct Complex {
double real, imag;
Complex() : real(0), imag(0) {}
Complex(double re, double im) : real(re), imag(im) {};
inline Complex operator + (const Complex & b) { return Complex(real + b.real, imag + b.imag); }
inline Complex operator - (const Complex & b) { return Complex(real - b.real, imag - b.imag); }
inline Complex operator * (const Complex & b) { return Complex(real * b.real - imag * b.imag, real * b.imag + imag * b.real); }
};
typedef std::vector<Complex> Vector;
const double PI = acos(-1);
void FFT(Vector &v, int n, int inv) {
if (n == 1) return; // 递归边界,只有一个元素,不做变换
// 奇偶变化为两个向量
int mid = n >> 1;
Vector even(mid), odd(mid);
for (int i(0); i < n; i += 2) {
even[i >> 1] = v[i], odd[i >> 1] = v[i + 1];
}
// 递归操作
FFT(even, mid, inv), FFT(odd, mid, inv);
// 进行合并操作
// 定义基本 omega
Complex omega(cos(PI * 2 / n), inv * sin(PI * 2 / n));
// 当前旋转因子
Complex w(1, 0);
for (int i(0); i < mid; ++i, w = w * omega) {
v[i] = even[i] + w * odd[i];
v[i + mid] = even[i] - w * odd[i];
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0), std::cout.tie(0);
int n, m;
std::cin >> n >> m;
// 获取最终的长度,必须是 2 的次幂,且比两个向量卷起来要长
int O(1);
while (O <= m + n) O <<= 1;
// std::cout << PI << " " << O << std::endl;
Vector A(O), B(O);
for (int i(0); i <= n; ++i) std::cin >> A[i].real;
for (int i(0); i <= m; ++i) std::cin >> B[i].real;
FFT(A, O, 1);
FFT(B, O, 1);
// 我们单点相乘,然后进行逆变换,求出每一项的系数
for (int i(0); i < O; ++i) A[i] = A[i] * B[i];
FFT(A, O, -1);
// 最后进行输出
// 记得两个东西卷起来之后是 n + m 次的
for (int i(0); i <= n + m; ++i) {
// 这里是向上取整?
std::cout << (long long)(A[i].real / O + 0.5) << ' ';
} std::cout << std::flush;
return 0;
}
复制我不知道为什么网上这么多写递归版本的都是错的。
例如本题第一篇题解,其实并不是方法有问题,是他的写法错了。
例如知乎上的一篇文章,其在递归时的边界是有问题的。虽然说不影响正确性……
链接:快速傅里叶变换 - 星夜
当然,还是有代码正确,但是代码……
有一个不算优化的优化。考虑每一层所需要的空间是固定的。所以考虑预先分配 \(O(n \log n)\) 的空间,然后直接使用即可。
在运行FFT的递归版本时,可以观察到递归树如下:

如果我们把初始向量 \(a\) 中的元素按照其在叶子中出现的次序进行安排,就可以对递归过程进行追踪,不过是自底向上,而非自顶向下。
回顾 FFT 合并时的代码:
for (int i(0); i < mid; ++i, w = w * omega) {
v[i] = even[i] + w * odd[i];
v[i + mid] = even[i] - w * odd[i];
}
复制在这个循环中,我们只用到了两个值:even[i], odd[i],得到了两个值:v[i], v[i + mid]。我们利用一种图示表示:

我们称这个操作为蝴蝶操作。
为了简化草图,我们采用另一种方式表达:

那么整个计算FFT的过程可以通过此图表示:
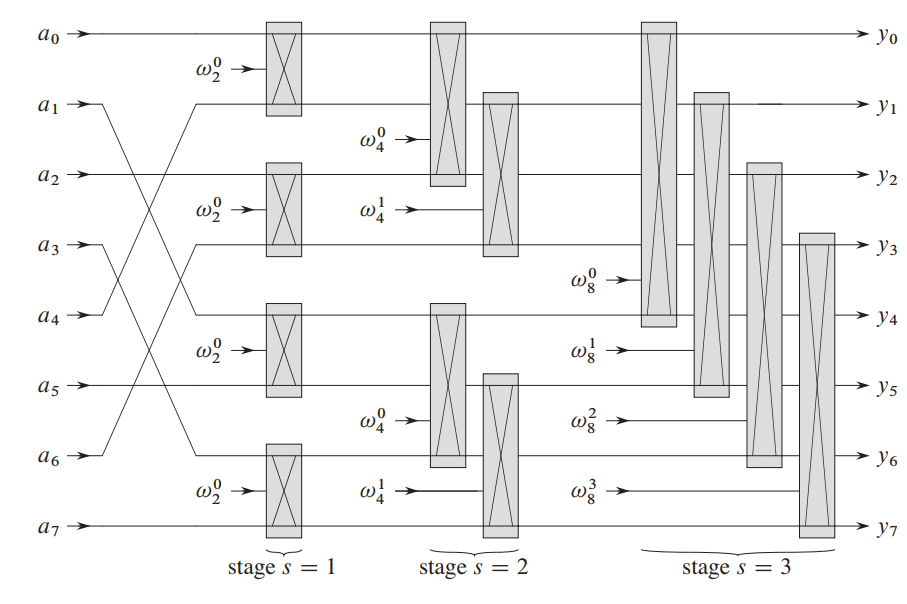
这个地方确实比较绕,难以通过语言表述,不过通过上面4张图,请读者停下稍微悟一悟。
其实从第一个递归的图中,我们已经可以发现初始值的规律了:
我们通过观察其二进制得出答案:下标的二进制恰好和目标二进制互为倒序。
一共只有 \(log(n)\) 位!也就是保证所有数拥有一样多的比特位。
也就是说当 \(n = 8\) 时 rev[3] = rev[0b011] = 0b110 = 6, \(\log8 = 4\)
我们考虑可以通过 DP 在 \(O(n)\) 内实现。
假设我们已经处理完了 \(1 \sim n-1\) 的所有 \(rev\)。
考虑 \(n = (abcd)_2\),此时我们已经知道了 \(rev[(0abc)_2] = (cba0)_2\),需要 \(rev[(abcd)_2] = (dcba)_2\)
通过瞪眼法,我们可以轻易的得出
\(rev[(abcd)_2] = (dcba)_2 = (rev[(0abc)_2]>>1)\ | \ ((d\&1)<<3)\)
改写为递推式即是:
dp[x] = (dp[x>>1] >> 1) | ((x&1) << (log2(n) - 1))
参考代码:
#include <complex>
#include <iostream>
#include <algorithm>
#include <vector>
struct Complex {
double real, imag;
Complex() : real(0), imag(0) {}
Complex(double re, double im) : real(re), imag(im) {};
inline Complex operator + (const Complex & b) { return Complex(real + b.real, imag + b.imag); }
inline Complex operator - (const Complex & b) { return Complex(real - b.real, imag - b.imag); }
inline Complex operator * (const Complex & b) { return Complex(real * b.real - imag * b.imag, real * b.imag + imag * b.real); }
};
typedef std::vector<Complex> Vector;
const double PI = acos(-1);
int O(1), logO(0);
void FFT(std::vector<int> &rev, Vector &v, int inv) {
for (int i(0); i < O; ++i) {
if (i < rev[i]) std::swap(v[i], v[rev[i]]);
}
// 第 log(k) 次合并,一共logO次
// 合并之后区间的长度为 k
for (int k(1); k < O; k <<= 1) {
Complex omega(cos(PI / k), inv * sin(PI / k));
for (int i(0); i < O; i += (k<<1)) { // 处理行
Complex w(1, 0);
for (int j = 0; j < k; ++j, w = w * omega) {
Complex s = v[i + j], t = v[i + j + k] * w;
v[i + j] = s + t, v[i + j + k] = s - t;
}
}
}
if (inv == -1) for (int i(0); i < O; ++i) v[i].real /= O;
}
int main() {
int n, m;
std::cin >> n >> m;
while (O <= n + m) O <<= 1, ++logO;
Vector A(O), B(O);
for (int i(0); i <= n; ++i) std::cin >> A[i].real;
for (int i(0); i <= m; ++i) std::cin >> B[i].real;
std::vector<int> rev(O);
for (int i(0); i < O; ++i) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (logO - 1));
FFT(rev, A, 1), FFT(rev, B, 1);
for (int i(0); i < O; ++i) A[i] = A[i] * B[i];
FFT(rev, A, -1);
for (int i(0); i <= n + m; ++i) {
std::cout << (long long)(A[i].real + 0.1) << ' '; // 向上取整
} std::cout << std::flush;
return 0;
}
复制那么恭喜你,大概是明白了 FFT 了吧!
快速数论变换我们可以类比快速傅里叶变换。只是将复数优化为了取模实数。
在模 \(p\) 意义下,会存在 \(a^{(p-1)} \equiv 1 \pmod p\)。
于是我们找到 \(\Z_p\) 中的一个原根 \(g\)。
可以参考:算法学习笔记(11): 原根 - jeefy - 博客园
满足:
\[\begin{aligned} \forall x \in [1, \varphi(p)), g^x \not\equiv 1 \pmod p \\ g^{\varphi(p)} \equiv 1 \pmod p \end{aligned} \]的数 \(g\) 即是 \(\Z_p\) 中的一个原根。
那么如何构造一个满足单位根性质的数?
令 \(v = \varphi(p)\),考虑:
显然,有 \(g_n \equiv 1 \pmod p\)
后文中为了方便,就不写后面的 \(\pmod p\) 了。
如果 n 不能整除 v 怎么办?凉拌
这也就是我们为什么把模数设为 998244353 = 119*2^{23} + 1 或者 167772161 = 5*2^{25}+1
那么我们来证明其满足作为单位根需要的三个性质:
消去:\(w_{dn}^{dk} = w_n^k\)
证明:考虑展开即可:\(w_{dn}^{dk} = g^{\frac v{dn} dk} = g^{\frac nk}\)
折半:\((w_n^{k+\frac n2})^2 = w_n^{2k + n} = w_n^{2k} = w_{\frac n2}^k\)
求和:\(\sum_{i=0}^{n-1} (\omega_n^k)^i = 0\)
证明:也考虑等比数列:
\[\begin{aligned} \sum_{i=0}^{n-1} (\omega_n^k)^i &= \cfrac {(w_n^k)^n - 1}{w_n^k - 1} \\ &= \cfrac {(w_n^n)^k - 1}{w_n^k - 1} \\ &= \cfrac {1^k - 1}{w_n^k - 1} = 0 \end{aligned} \]这过程怎么一模一样……
那么我们可以将单位根替换,进行变换了!
说实话,代码几乎是一模一样的……
const int MOD = 998244353, g = 3, ig = 332748118;
int O(1), logO(0);
typedef vector<long long> vec;
typedef vector<int> ivec;
void NTT(ivec &rev, vec &v, int inv) {
for (int i(0); i < O; ++i) {
if (rev[i] < i) std::swap(v[i], v[rev[i]]);
}
// 第 log(k) 次合并
for (int k(1); k < O; k <<= 1) {
long long omega = qpow((long long)(~inv ? g : ig), (MOD - 1) / (k << 1), MOD);
for (int i(0); i < O; i += (k << 1)) {
long long w(1);
for (int j(0); j < k; ++j, w = w * omega % MOD) {
long long s = v[i + j], t = w * v[i + j + k];
v[i + j] = (s + t) % MOD, v[i + j + k] = ((s - t) % MOD + MOD) % MOD;
}
}
}
if (inv == -1) {
for (int iv(qpow((long long)O, MOD - 2, MOD)), i(0); i < O; ++i) {
v[i] = v[i] * iv % MOD;
}
}
}
复制而且由于没有了复数,常数会小很多(比FFT快)