通常做题思路:问题转化为流网络,再通过最大流 / 最小割 / 费用流与问题之间的数量关系,求解出原问题。
网络流于其他算法不同,概念定理需要熟记于心,否则后面做题会有很大的障碍。
一个流网络记作 \(G=(V,E)\),其中 \(V\) 表示点集,\(E\) 表示边集。对于 \(\forall (u,v)\in E\),都有一个容量记作 \(c(u,v)\)。由于是一张流网络,那肯定还应该有汇点与源点,通常记作 \(s,t\)。
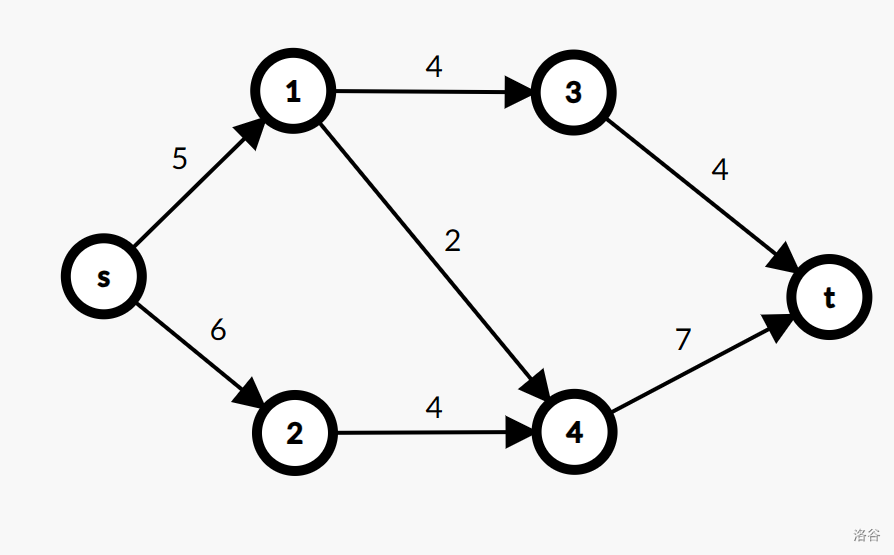
如图,这就是一张流网络。
对于每一个流网络,满足以下 \(2\) 个条件为可行流:
容量限制
记作:\(0\le f(u,v) \le c(u,v)\),即流经每条边的流量不能超过他的限制。
流量守恒
记作:\(\sum_{(v,x)\in E}f(v,x)=\sum_{(x,v)\in E}f(x,v)\),即除了源点与汇点之外,流入点 \(i\) 的总流量 \(=\) 流出点 \(i\) 的总流量。
可行流的流量 \(|f|\),是指从源点流出的总流量。
即:\(|f|=\sum_{(s,v)\in E}f(s,v)-\sum_{(v,s)\in E}f(v,s)\)
一般来说,残留网络记作 \(G_f=(V,E+!E)\),其中 \(V,E\) 是源网络的边集和点集,\(!E\) 表示 \(E\) 中的所有反向边。
容量:
\(f\) 为原网络的可行流,\(f'\) 为残留网络的可行流。
则有:\(f+f'\) 也是 \(G\) 的一个可行流且 \(|f+f'|=|f|+|f'|\)
证明:定义 \(f_{n}=f+f'\),则 \(f_n(u,v)=f(u,v)+f'(u,v)\)(注意这里只考虑正向边),为了证明也是一个可行流,无非从 \(2\) 方面:容量限制和流量守恒。
容量限制:\(f'(u,v)\le c'(u,v)=c(u,v)-f(u,v)\),所以 \(f(u,v)+f'(u,v)\le c(u,v)\)
流量守恒:因为 \(f(u,v)\) 满足流量守恒,\(f'(u,v)\) 也满足流量守恒,所以 \(f(u,v)+f'(u,v)\) 也满足流量守恒(这里只是略证,更多细节大家可以展开观察)。
在残留网络沿着容量大于 \(0\) 的边如果能够走到终点,这条路径称为增广路径。(注意:增广路径只是一条路径,而非一个网络)
将点集 \(V\) 分成不重叠 \(S\) 和 \(T\), 使得源点在\(S\),汇点在 \(T\)。
\(c(S,T)=\sum_{u\in S}\sum_{v\in T} c(u,v)\)
最小割: 最小的割的容量
\(f(S,T)=\sum_{u\in S}\sum_{v\in T} f(u,v)-\sum_{v\in S}\sum_{u\in T} f(u,v)\)
性质1: \(\forall [S,T], f(S,T)\le c(S,T)\)
证明: 由于 \(f(u,v)\) 是大于等于 \(0\) 的,所以 \(f(S,T)\le \sum_{u\in S}\sum_{v\in T} f(u,v)\),又因为有容量,所以一定 \(\le \sum_{u\in S}\sum_{v\in T} c(u,v)\) ,故 \(\forall [S,T], f(S,T)\le c(S,T)\)
性质2: \(\forall [S,T], f(S,T)= |f|\)
证明2:
\(f(X,Y)=\sum_{u\in X}\sum_{v\in Y} f(u,v)-\sum_{v\in X}\sum_{u\in Y} f(u,v)\)
则:\(f(X,Y)=-f(Y,X)\), \(f(X,X)=0\),\(f(Z,X\cup Y)=f(Z,X)+f(Z,Y), X\cap Y= \varnothing\)
那么有:
那么 \(|f|=f(S,T)\le c(S,T)\)
即,\(|f|\le c(S,T)\);故,最大流 \(\le\) 最小割
(1)可行流 \(f\) 是最大流
(2)\(G_f\) 中不存在增广路
(3)\(|f|=c(S,T)\)
在三个条件中,仅需知道 \(1\) 个,就能够推出另外 \(2\) 个,证明略。